Индекс Джини можно выразить через площадь $A$ под кривой Лоренца:
\[
G \;=\; 1 - 2A.
\]
Отсюда условие «неравенство не выросло» эквивалентно
\[
G_{\text{после}} \le G_{\text{до}}
\quad\Longleftrightarrow\quad
A_{\text{после}} \ge A_{\text{до}}.
\]
Мы будем сравнивать площади под кривыми Лоренца до и после исправления бага,
не используя формулу для $G$.
1. Распределения "до" и "после"
Пусть у Алекса $m$ друзей. Тогда всего в гильдии $n = m+1$ человек.
До вмешательства администратора:
Сначала у одного друга было $5$ золота, остальные (включая Алекса) - по $0$.
После подземелья каждый друг получил $4$ золота, Алекс ничего не получил.
Итого до выдачи 21 золота Алексу: у одного друга: $5+4 = 9$, у остальных $m-1$ друзей: по $4$, у Алекса: $0$.
Отсортированное распределение:
\[
(0,\underbrace{4,\dots,4}_{m-1\;\text{человек}},9).
\]
Общий доход:
\[
I_{\text{до}} = 0+4(m-1)+9 = 4m+5.
\]
Выделим три группы:
Группа $1$: Алекс (1 человек), доход $0$.
Группа $2$: остальные друзья с $4$ (их $m-1$), суммарный доход $4(m-1)$.
Группа $3$: самый богатый друг с $9$.
Доли населения:
\[
x_1^{\text{(до)}} = \frac{1}{n},\qquad
x_2^{\text{(до)}} = \frac{1 + (m-1)}{n} = \frac{m}{n},\qquad
x_3^{\text{(до)}} = 1.
\]
Доли суммарного дохода:
\[
y_1^{\text{(до)}} = \frac{0}{T_{\text{до}}} = 0,\qquad
y_2^{\text{(до)}} = \frac{4(m-1)}{4m+5},\qquad
y_3^{\text{(до)}} = 1.
\]
Кривая Лоренца до выдачи проходит через точки
\[
(0,0),\quad
\left(x_1^{\text{(до)}},y_1^{\text{(до)}}\right) = \left(\frac1n,0\right),\quad
\left(x_2^{\text{(до)}},y_2^{\text{(до)}}\right) = \left(\frac{m}{n},\frac{4(m-1)}{4m+5}\right),\quad
(1,1).
\]
Это ломаная из трёх отрезков (см. иллюстрацию в конце).
После вмешательства администратора
Администратор выдал Алексу $21$ золото.
Тогда распределение становится:
\[
(\underbrace{4,\dots,4}_{m-1\;\text{человек}},9,21),
\]
так как теперь Алекс самый богатый.
Общий доход:
\[
I_{\text{после}} = 4(m-1)+9+21 = 4m+26.
\]
Группы:
Группа $1$: $m-1$ человек с доходом $4$, суммарный доход $4(m-1)$.
Группа $2$: один человек с $9$.
Группа $3$: Алекс с $21$.
Доли населения:
\[
x_1^{\text{(после)}} = \frac{m-1}{n},\qquad
x_2^{\text{(после)}} = \frac{m}{n},\qquad
x_3^{\text{(после)}} = 1.
\]
Суммарные доходы первых $k$ групп:
\[
\text{Группа 1: }4(m-1),
\qquad
\text{Группы 1+2: }4(m-1)+9 = 4m+5,
\qquad
\text{Все: }4m+26.
\]
Соответствующие доли дохода:
\[
y_1^{\text{(после)}} = \frac{4(m-1)}{4m+26},\qquad
y_2^{\text{(после)}} = \frac{4m+5}{4m+26},\qquad
y_3^{\text{(после)}} = 1.
\]
Кривая Лоренца после выдачи проходит через точки
\[
(0,0),\quad
\left(x_1^{\text{(после)}},y_1^{\text{(после)}}\right)
= \left(\frac{m-1}{n},\frac{4(m-1)}{4m+26}\right),\quad
\left(x_2^{\text{(после)}},y_2^{\text{(после)}}\right)
= \left(\frac{m}{n},\frac{4m+5}{4m+26}\right),\quad
\]
Опять получаем ломаную из трёх отрезков.
2. Площади под кривыми Лоренца: треугольник + две трапеции
Площадь до исправления бага:
Точки:
\[
(0,0),\quad
\left(\frac{1}{n},0\right),\quad
\left(\frac{m}{n},y_2\right),\quad
\]
где
\[
y_2 := y_2^{\text{(до)}} = \frac{4(m-1)}{4m+5}.
\]
Первый отрезок от $x=0$ до $x=\frac1n$ идёт по оси $x$, высота нулевая, площадь равна $0$.
Вторая фигура - трапеция между $x=\frac{1}{n}$ и $x=\frac{m}{n}$, нижняя высота $0$, верхняя - $y_2$, основание:
\[
\frac{m}{n} - \frac{1}{n} = \frac{m-1}{n}.
\]
Площадь:
\[
S_2^{\text{(до)}} = \frac{\frac{m-1}{n}\cdot (0+y_2)}{2}
= \frac{m-1}{2n}\,y_2.
\]
Третья фигура - трапеция между $x=\frac{m}{n}$ и $x=1$, высоты $y_2$ и $1$, основание
\[
1 - \frac{m}{n} = \frac{n-m}{n} = \frac{1}{n}.
\]
Площадь:
\[
S_3^{\text{(до)}} = \frac{\frac{1}{n}\cdot (y_2+1)}{2}
= \frac{y_2+1}{2n}.
\]
Таким образом, общая площадь:
\[
A_{\text{до}} = S_2^{\text{(до)}} + S_3^{\text{(до)}}
= \frac{m-1}{2n}\,y_2 + \frac{y_2+1}{2n}.
\]
Подставляем $n=m+1$ и $y_2=\dfrac{4(m-1)}{4m+5}$:
\[
A_{\text{до}}
= \frac{1}{2(m+1)}
\left(
(m-1)\cdot \frac{4(m-1)}{4m+5} + \frac{4(m-1)}{4m+5} + 1
\right).
\]
Складываем первые два слагаемых:
\[
(m-1)\cdot 4(m-1) + 4(m-1)
= 4(m-1)\bigl((m-1)+1\bigr) = 4(m-1)m.
\]
Тогда
\[
A_{\text{до}}
= \frac{1}{2(m+1)}
\left(
\frac{4(m-1)m}{4m+5} + 1
\right)
= \frac{1}{2(m+1)}\cdot \frac{4(m-1)m + (4m+5)}{4m+5}.
\]
Числитель:
\[
4(m-1)m + 4m + 5 = 4m^2 - 4m + 4m + 5 = 4m^2 + 5.
\]
Таким образом,
\[
A_{\text{до}}
= \frac{4m^2 + 5}{2(m+1)(4m+5)}\]
Площадь после исправления бага:
Точки:
\[
(0,0),\quad
\left(\frac{m-1}{n},y_1'\right),\quad
\left(\frac{m}{n},y_2'\right),\quad
\]
где
\[
y_1' = y_1^{\text{(после)}} = \frac{4(m-1)}{4m+26},
\qquad
y_2' = y_2^{\text{(после)}} = \frac{4m+5}{4m+26}.
\]
Теперь уже первый отрезок даёт ненулевую площадь: треугольник под отрезком между $x=0$ и $x=\frac{m-1}{n}$.
Треугольник от $0$ до $\frac{m-1}{n}$, высота на правом конце $y_1'$, площадь:
\[
S_1^{\text{(после)}} = \frac{1}{2}\cdot \frac{m-1}{n}\cdot y_1'
= \frac{m-1}{2n}\,y_1'.
\]
Первая трапеция между $x=\frac{m-1}{n}$ и $x=\frac{m}{n}$, высоты $y_1'$ и $y_2'$, основание
\[
\frac{m}{n} - \frac{m-1}{n} = \frac{1}{n},
\]
площадь:
\[
S_2^{\text{(после)}}
= \frac{1}{2}\cdot \frac{1}{n}\cdot (y_1' + y_2')
= \frac{y_1'+y_2'}{2n}.
\]
Вторая трапеция между $x=\frac{m}{n}$ и $x=1$, высоты $y_2'$ и $1$, основание
\[
1 - \frac{m}{n} = \frac{1}{n},
\]
площадь:
\[
S_3^{\text{(после)}}
= \frac{1}{2}\cdot \frac{1}{n}\cdot (y_2'+1)
= \frac{y_2'+1}{2n}.
\]
Таким образом,
\[A_{\text{после}}
= S_1^{\text{(после)}} + S_2^{\text{(после)}} + S_3^{\text{(после)}}
= \frac{m-1}{2n}\,y_1' + \frac{y_1'+y_2'}{2n} + \frac{y_2'+1}{2n}.\]
или
\[
A_{\text{после}}
= \frac{1}{2n}\Bigl((m-1)y_1' + y_1' + y_2' + y_2' + 1\Bigr)
= \frac{1}{2n}\bigl(m y_1' + 2y_2' + 1\bigr).
\]
Подставляем $n=m+1$, $y_1' = \dfrac{4(m-1)}{4m+26}$, $y_2' = \dfrac{4m+5}{4m+26}$:
\[
A_{\text{после}}
= \frac{1}{2(m+1)}
\left(
m\cdot \frac{4(m-1)}{4m+26}
+ 2\cdot \frac{4m+5}{4m+26}
+ 1
\right).
\]
Вынесем общий знаменатель $4m+26$ в скобке:
\[
A_{\text{после}}
= \frac{1}{2(m+1)}
\left(
\frac{4m(m-1) + 2(4m+5)}{4m+26}
+ 1
\right).
\]
Считаем числитель:
\[
4m(m-1) + 2(4m+5)
= 4m^2 - 4m + 8m + 10
= 4m^2 + 4m + 10.
\]
Тогда
\[
A_{\text{после}}
= \frac{1}{2(m+1)}
\left(
\frac{4m^2 + 4m + 10}{4m+26}
+ 1
\right)
= \frac{1}{2(m+1)}\cdot
\frac{4m^2 + 4m + 10 + (4m+26)}{4m+26}.
\]
Числитель:
\[
4m^2 + 4m + 10 + 4m + 26
= 4m^2 + 8m + 36
= 4(m^2 + 2m + 9).
\]
Получаем
\[
A_{\text{после}}
= \frac{1}{2(m+1)}\cdot
\frac{4(m^2 + 2m + 9)}{4m+26}
= \frac{2(m^2 + 2m + 9)}{(m+1)(4m+26)}.
\]
Заметим, что $4m+26 = 2(2m+13)$:
\[
A_{\text{после}}
= \frac{m^2+2m+9}{(m+1)(2m+13)}
\]
3. Неравенство площадей и максимальное $m$
Требуем, чтобы индекс Джини не увеличился:
\[
A_{\text{после}} \ge A_{\text{до}}.
\]
Подставляем найденные выражения:
\[
\frac{m^2+2m+9}{(m+1)(2m+13)}
\;\ge\;
\frac{4m^2 + 5}{2(m+1)(4m+5)}.
\]
Заметим, что $(m+1)>0$ для $m\ge1$, поэтому можно сократить на $(m+1)$.
Перенесём всё в одну сторону и приведём к общему знаменателю,
но удобнее сразу перемножить ``крест-накрест'' (зная, что знаменатели положительны при $m\ge1$):
\[
2(m^2+2m+9)(4m+5) \;\ge\; (4m^2+5)(2m+13).
\]
Раскроем скобки.
Слева:
\[
(m^2+2m+9)(4m+5)
= 4m^3 + 5m^2 + 8m^2 + 10m + 36m + 45
= 4m^3 + 13m^2 + 46m + 45.
\]
Умножаем на $2$:
\[
\text{Левая часть} = 8m^3 + 26m^2 + 92m + 90.
\]
Справа:
\[
(4m^2+5)(2m+13)
= 8m^3 + 52m^2 + 10m + 65.
\]
Неравенство превращается в
\[
8m^3 + 26m^2 + 92m + 90
\;\ge\;
8m^3 + 52m^2 + 10m + 65.
\]
Вычитаем правую часть:
\[
0 \;\ge\; (8m^3+26m^2+92m+90) - (8m^3+52m^2+10m+65)
= -26m^2 + 82m + 25.
\]
То есть
\[
-26m^2 + 82m + 25 \ge 0
\quad\Longleftrightarrow\quad
26m^2 - 82m - 25 \le 0.
\]
Решим квадратное неравенство.
Сначала корни уравнения
\[
26m^2 - 82m - 25 = 0.
\]
Дискриминант:
\[
D = (-82)^2 - 4\cdot 26\cdot(-25)
= 6724 + 2600 = 9324 = 9\cdot 1036 = 9\cdot 4\cdot 259 = 36\cdot 259,
\]
значит
\[
\sqrt{D} = 6\sqrt{259}.
\]
Тогда
\[
m_{1,2} = \frac{82 \pm 6\sqrt{259}}{52}
= \frac{41 \pm 3\sqrt{259}}{26}.
\]
\[
m_1 \approx -0{,}28,\qquad m_2 \approx 3{,}43.
\]
Так как коэффициент при $m^2$ положителен, неравенство
\[
26m^2 - 82m - 25 \le 0
\]
выполняется между корнями:
\[
m_1 \le m \le m_2.
\]
При $m\ge1$ остаётся
\[
1 \le m \le 3{,}43\dots
\]
то есть целые $m$:
\[
m = 1,\ 2,\ 3.
\]
Но нас интересует максимально возможное $m$, значит $m_{\max} = 3.$
Тогда максимальное количество людей в гильдии - 4.
4. Иллюстрация кривых Лоренца (пример для $m=3$)
Ниже — пример кривых Лоренца до и после для случая $m=3$ (всего $n=4$ человека).
Числа на рисунке не строго по масштабу, рисунок иллюстративный (синяя и красная кривая на среднем участке в действительности накладываются друг на друга).
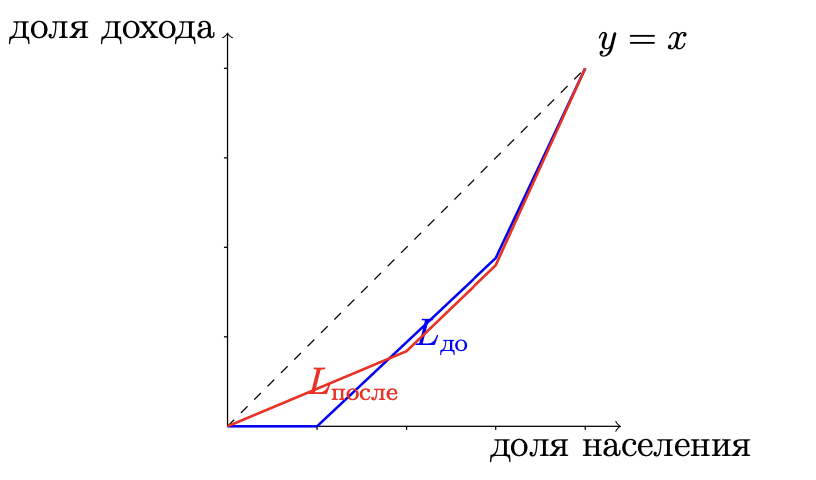
На рисунке видно, что кривая $L_{\text{после}}$ (красная) не лежит ниже $L_{\text{до}}$ (синяя) при $m=3$,
что соответствует условию $A_{\text{после}}\ge A_{\text{до}}$ для этого случая.
