Канал об олимпиадной экономике: https://t.me/economybyanton
1) Общение сведения:
Индекс Джини $G$ определяется как
\[
G = \dfrac{S}{0.5} = 2S,
\]
где $S$ - площадь области между диагональю и кривой Лоренца.
Индекс Робин Гуда $H$ можно вычислить как максимальное вертикальное расстояние между кривой Лоренца и линией абсолютного равенства:
\[
H = \max_{0\le x \le 1}\bigl(d(x)\bigr)=\max_{0\le x \le 1}\bigl(x - y(x)\bigr),
\]
где $y(x)$ - уравнение кривой Лоренца, $d$ -- вертикальное расстояние между линией абсолютного равенства и кривой Лоренца.
2) Верхняя оценка: $G \leqslant 2H$.
Из метода рассчета индекса Робин Гуда имеем неравенство:
\[
d(x) \leqslant H \quad \text{для всех } x\in[0,1].
\]
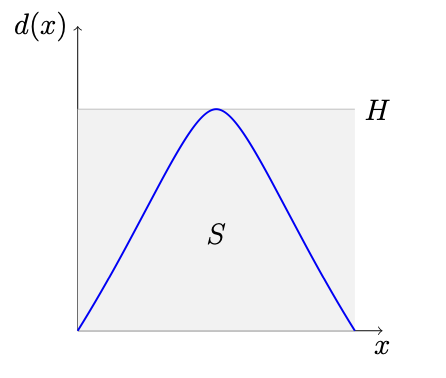
Это означает, что график функции $d(x)$ целиком лежит под горизонтальной прямой $y=H$.
Следовательно, площадь под графиком $d(x)$ на отрезке $[0,1]$ не превосходит площади прямоугольника ширины $1$ и высоты $H$, откуда следует что
\[
S \le H.
\]
или
\[
G = 2S \le 2H.
\]
3) Нижняя оценка: $H \leqslant G$.
Кривая Лоренца по определению выпукла вверх: её график лежит не выше любой своей хорды.
Понимая, что $d(x) = x - y(x)$ и кривая Лоренца по определению выпукла вверх, $d(x)$ - вогнутая функция (разность линейной функции и выпуклой функции).
Обозначим точку, в которой $d(x)$ достигает максимума, через $x_0$, т.е. $ d(x_0) = H.$
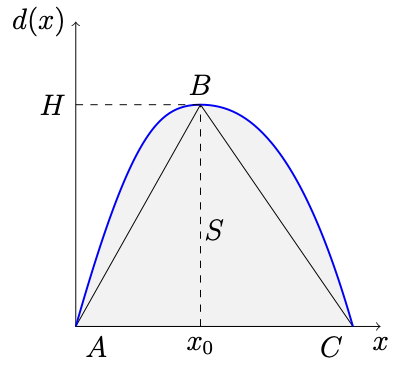
Рассмотрим три точки на графике $d(x)$:
\[
A=(0,0),\quad B=(x_0,H),\quad C=(1,0).
\]
Из вогнутости $d(x)$ следует:
1. на отрезке $[0,x_0]$ график $d(x)$ лежит не ниже хорды $AB$;
2. на отрезке $[x_0,1]$ график $d(x)$ лежит не ниже хорды $BC$.
Значит, площадь под графиком $d(x)$ на $[0,1]$ не меньше площади под ломаной, проходящей через точки $A$, $B$, $C$, а последняя равна площади треугольника $ABC$.
У треугольника $ABC$ основание по оси $x$ равно $1$ (от $0$ до $1$), а высота по оси $y$ равна $H$. Поэтому его площадь равна
\[
S_{ABC} = \frac{1}{2}\cdot 1 \cdot H = \frac{H}{2}.
\]
Так как график $d(x)$ не ниже ломаной, площадь под графиком $d(x)$ не меньше $S_{ABC}=\frac{H}{2}$. Откуда
\[
G = 2S \geqslant 2\cdot \frac{H}{2} = H.
\]
4) Вывод: для любых допустимых кривых Лоренца всегда выполнется неравенство
\[
H \leqslant G \leqslant 2H.
\]


 3) Нижняя оценка: $H \leqslant G$.
Кривая Лоренца по определению выпукла вверх: её график лежит не выше любой своей хорды.
Понимая, что $d(x) = x - y(x)$ и кривая Лоренца по определению выпукла вверх, $d(x)$ - вогнутая функция (разность линейной функции и выпуклой функции).
Обозначим точку, в которой $d(x)$ достигает максимума, через $x_0$, т.е. $ d(x_0) = H.$
3) Нижняя оценка: $H \leqslant G$.
Кривая Лоренца по определению выпукла вверх: её график лежит не выше любой своей хорды.
Понимая, что $d(x) = x - y(x)$ и кривая Лоренца по определению выпукла вверх, $d(x)$ - вогнутая функция (разность линейной функции и выпуклой функции).
Обозначим точку, в которой $d(x)$ достигает максимума, через $x_0$, т.е. $ d(x_0) = H.$
 Рассмотрим три точки на графике $d(x)$:
\[
A=(0,0),\quad B=(x_0,H),\quad C=(1,0).
\]
Из вогнутости $d(x)$ следует:
1. на отрезке $[0,x_0]$ график $d(x)$ лежит не ниже хорды $AB$;
2. на отрезке $[x_0,1]$ график $d(x)$ лежит не ниже хорды $BC$.
Значит, площадь под графиком $d(x)$ на $[0,1]$ не меньше площади под ломаной, проходящей через точки $A$, $B$, $C$, а последняя равна площади треугольника $ABC$.
У треугольника $ABC$ основание по оси $x$ равно $1$ (от $0$ до $1$), а высота по оси $y$ равна $H$. Поэтому его площадь равна
\[
S_{ABC} = \frac{1}{2}\cdot 1 \cdot H = \frac{H}{2}.
\]
Так как график $d(x)$ не ниже ломаной, площадь под графиком $d(x)$ не меньше $S_{ABC}=\frac{H}{2}$. Откуда
\[
G = 2S \geqslant 2\cdot \frac{H}{2} = H.
\]
4) Вывод: для любых допустимых кривых Лоренца всегда выполнется неравенство
\[
H \leqslant G \leqslant 2H.
\]
Рассмотрим три точки на графике $d(x)$:
\[
A=(0,0),\quad B=(x_0,H),\quad C=(1,0).
\]
Из вогнутости $d(x)$ следует:
1. на отрезке $[0,x_0]$ график $d(x)$ лежит не ниже хорды $AB$;
2. на отрезке $[x_0,1]$ график $d(x)$ лежит не ниже хорды $BC$.
Значит, площадь под графиком $d(x)$ на $[0,1]$ не меньше площади под ломаной, проходящей через точки $A$, $B$, $C$, а последняя равна площади треугольника $ABC$.
У треугольника $ABC$ основание по оси $x$ равно $1$ (от $0$ до $1$), а высота по оси $y$ равна $H$. Поэтому его площадь равна
\[
S_{ABC} = \frac{1}{2}\cdot 1 \cdot H = \frac{H}{2}.
\]
Так как график $d(x)$ не ниже ломаной, площадь под графиком $d(x)$ не меньше $S_{ABC}=\frac{H}{2}$. Откуда
\[
G = 2S \geqslant 2\cdot \frac{H}{2} = H.
\]
4) Вывод: для любых допустимых кривых Лоренца всегда выполнется неравенство
\[
H \leqslant G \leqslant 2H.
\]
