Канал об олимпиадной экономике: https://t.me/economybyanton
а-1) Случай двух групп
Пусть кривая Лоренца состоит из двух отрезков, проходящих через точки $(0,0)$, $(a,b)$ и $(1,1)$, где $(a,b)$ — точка излома.
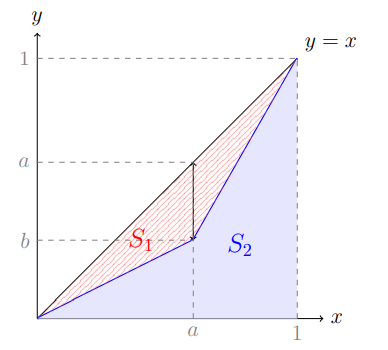
Индекс Джини вычисляется как:
\[
G = \frac{S_1}{S_1 + S_2} = \frac{0.5 - S_2}{0.5} = 1 - 2S_2 = 1 - 2\cdot\left(\frac{ab}{2} + \frac{b+1}{2}(1-a)\right) = a - b
\]
Данная формула является общеизвестной и может быть использована без доказательства.
Теперь выразим индекс Робин Гуда. В условиях абсолютного равенства бедная группа должна иметь долю $a$ совокупного дохода, тогда как до перераспределения она имела долю $b$. Следовательно, необходимо перераспределить ровно $H = a - b$ совокупного дохода.
Таким образом, для двух групп:
\[
H = G = a - b
\]
а-2) Случай трёх групп
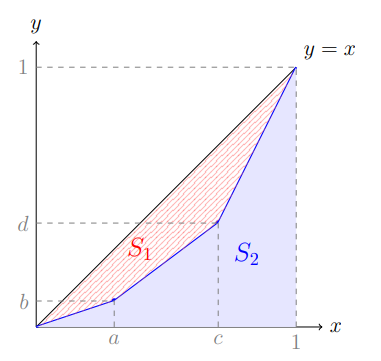
Пусть кривая Лоренца имеет изломы в точках $(a,b)$ и $(c,d)$. Площадь под кривой Лоренца:
\[
S_2 = \frac{ab}{2} + \frac{(b+d)(c-a)}{2} + \frac{(d+1)(1-c)}{2}
\]
Коэффициент Джини:
\[
G = 1 - 2S_2 = 1 - 2\cdot \left(\frac{ab}{2} + \frac{(b+d)(c-a)}{2} + \frac{(d+1)(1-c)}{2}\right) = c - d + ad - bc
\]
Выпишем данные по группам:
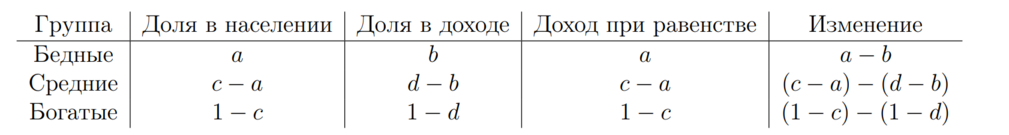
Столбец "Изменение" показывает, какую долю совокупного дохода нужно добавить (если значение положительно) или забрать (если отрицательно) для каждой группы. Заметим, что бедным всегда нужно добавлять доход, а у богатых — забирать. Для средних возможны два случая:
Первый случай: средние зарабатывают меньше среднего дохода общества ($(c - a) - (d - b) < 0$). Тогда нужно перераспределить $H = c - d$ от богатых к бедным и средним.
Второй случай: средние зарабатывают больше среднего дохода ($(c - a) - (d - b) > 0$). Тогда нужно перераспределить $H = a - b$ от богатых и средних к бедным.
Сравнение в первом случае:
\[
\begin{aligned}
&G \quad \text{vs.} \quad H \\
&c - d + ad - bc \quad \text{vs.} \quad c - d \\
&ad - bc \quad \text{vs.} \quad 0 \\
&\frac{d}{c} \quad \text{vs.} \quad \frac{b}{a}
\end{aligned}
\]
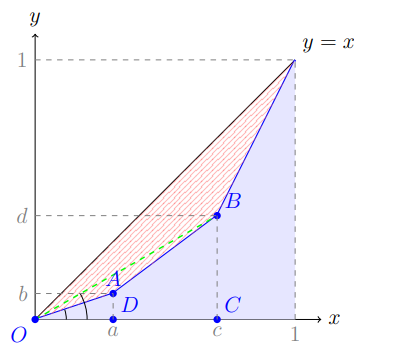
Так как кривая Лоренца выпукла, то $\frac{b}{a} = \tan\angle AOD < \frac{d}{c} = \tan\angle BOC$, откуда:
\[
\frac{d}{c} > \frac{b}{a} \quad \Rightarrow \quad G > H
\]
Сравнение во втором случае:
\[
\begin{aligned}
&G \quad \text{vs.} \quad H \\
&c - d + ad - bc \quad \text{vs.} \quad a - b \\
&(c - d + ad - bc) - (a - b) = [(c - a) - (d - b)](1 - b) + (a - b)(d - b)
\end{aligned}
\]
По условию второго случая:
$(c - a) - (d - b) > 0$ (средние имеют избыток дохода)
$1 - b > 0$,
$a - b > 0$,
$d - b > 0$
Все слагаемые положительны, следовательно:
\[
G - H > 0 \quad \Rightarrow \quad G > H
\]
Вывод: для трёх групп индекс Джини всегда больше индекса Робин Гуда.
а-3) Общий случай $n \geq 2$
Рассмотрим $n$-звенную кривую Лоренца и отметим граничную точку $(a,b)$, слева от которой располагаются жители, которым нужно добавить доход, а справа — те, у кого доход нужно уменьшить. Суммарно необходимо перераспределить долю $a - b$ совокупного дохода.
Теперь рассмотрим двузвенную кривую Лоренца с изломом в точке $(a,b)$ (зелёная ломаная). Для такой кривой индекс Джини равен индексу Робин Гуда и составляет $a - b$. Однако в силу выпуклости исходной кривой коэффициент Джини для вспомогательной кривой будет ниже, чем для исходной, при этом индексы Робин Гуда для обеих кривых совпадают.
Следовательно, коэффициент Джини для исходной кривой больше индекса Робин Гуда.
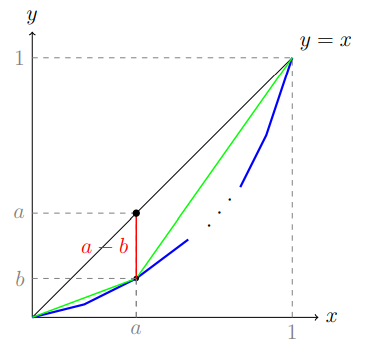
б) Гладкая кривая Лоренца
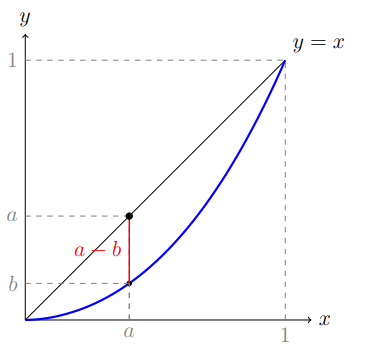
Аналогично рассмотрим новую кривую Лоренца, состоящую из двух отрезков, соединяющих точки $(0,0)$, $(a,b)$ и $(1,1)$, где $(a,b)$ — граничная точка (переход от нуждающихся в субсидии к тем, у кого доход нужно уменьшить). Для такой кусочно-линейной кривой индекс Робин Гуда равен индексу Джини и составляет $H = G = a - b$.
Поскольку построенная ломаная всюду лежит не ниже исходной кривой Лоренца (т.е. ближе к линии равенства), площадь между ней и диагональю превышает соответствующей площади для исходной кривой. Следовательно:
\[
G_{\text{исх}} > G_{\text{лом}} = H_{\text{лом}}
\]
В то же время, по построению, максимальное вертикальное отклонение у обеих кривых достигается в точке $(a,b)$ и равно $a - b$, поэтому:
\[
H_{\text{исх}} = H_{\text{лом}}
\]
Таким образом:
\[
G_{\text{исх}} > H_{\text{исх}}
\]
что доказывает неравенство между индексом Джини и индексом Робин Гуда для гладкой кривой Лоренца.


 Индекс Джини вычисляется как:
\[
G = \frac{S_1}{S_1 + S_2} = \frac{0.5 - S_2}{0.5} = 1 - 2S_2 = 1 - 2\cdot\left(\frac{ab}{2} + \frac{b+1}{2}(1-a)\right) = a - b
\]
Данная формула является общеизвестной и может быть использована без доказательства.
Теперь выразим индекс Робин Гуда. В условиях абсолютного равенства бедная группа должна иметь долю $a$ совокупного дохода, тогда как до перераспределения она имела долю $b$. Следовательно, необходимо перераспределить ровно $H = a - b$ совокупного дохода.
Таким образом, для двух групп:
\[
H = G = a - b
\]
а-2) Случай трёх групп
Индекс Джини вычисляется как:
\[
G = \frac{S_1}{S_1 + S_2} = \frac{0.5 - S_2}{0.5} = 1 - 2S_2 = 1 - 2\cdot\left(\frac{ab}{2} + \frac{b+1}{2}(1-a)\right) = a - b
\]
Данная формула является общеизвестной и может быть использована без доказательства.
Теперь выразим индекс Робин Гуда. В условиях абсолютного равенства бедная группа должна иметь долю $a$ совокупного дохода, тогда как до перераспределения она имела долю $b$. Следовательно, необходимо перераспределить ровно $H = a - b$ совокупного дохода.
Таким образом, для двух групп:
\[
H = G = a - b
\]
а-2) Случай трёх групп
 Пусть кривая Лоренца имеет изломы в точках $(a,b)$ и $(c,d)$. Площадь под кривой Лоренца:
\[
S_2 = \frac{ab}{2} + \frac{(b+d)(c-a)}{2} + \frac{(d+1)(1-c)}{2}
\]
Коэффициент Джини:
\[
G = 1 - 2S_2 = 1 - 2\cdot \left(\frac{ab}{2} + \frac{(b+d)(c-a)}{2} + \frac{(d+1)(1-c)}{2}\right) = c - d + ad - bc
\]
Выпишем данные по группам:
Пусть кривая Лоренца имеет изломы в точках $(a,b)$ и $(c,d)$. Площадь под кривой Лоренца:
\[
S_2 = \frac{ab}{2} + \frac{(b+d)(c-a)}{2} + \frac{(d+1)(1-c)}{2}
\]
Коэффициент Джини:
\[
G = 1 - 2S_2 = 1 - 2\cdot \left(\frac{ab}{2} + \frac{(b+d)(c-a)}{2} + \frac{(d+1)(1-c)}{2}\right) = c - d + ad - bc
\]
Выпишем данные по группам:
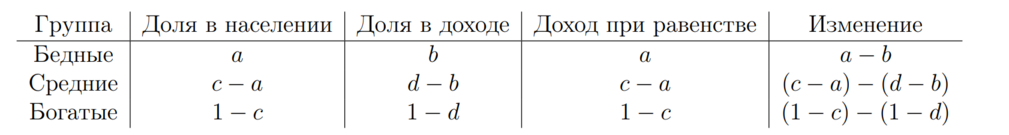 Столбец "Изменение" показывает, какую долю совокупного дохода нужно добавить (если значение положительно) или забрать (если отрицательно) для каждой группы. Заметим, что бедным всегда нужно добавлять доход, а у богатых — забирать. Для средних возможны два случая:
Первый случай: средние зарабатывают меньше среднего дохода общества ($(c - a) - (d - b) < 0$). Тогда нужно перераспределить $H = c - d$ от богатых к бедным и средним.
Второй случай: средние зарабатывают больше среднего дохода ($(c - a) - (d - b) > 0$). Тогда нужно перераспределить $H = a - b$ от богатых и средних к бедным.
Сравнение в первом случае:
\[
\begin{aligned}
&G \quad \text{vs.} \quad H \\
&c - d + ad - bc \quad \text{vs.} \quad c - d \\
&ad - bc \quad \text{vs.} \quad 0 \\
&\frac{d}{c} \quad \text{vs.} \quad \frac{b}{a}
\end{aligned}
\]
Столбец "Изменение" показывает, какую долю совокупного дохода нужно добавить (если значение положительно) или забрать (если отрицательно) для каждой группы. Заметим, что бедным всегда нужно добавлять доход, а у богатых — забирать. Для средних возможны два случая:
Первый случай: средние зарабатывают меньше среднего дохода общества ($(c - a) - (d - b) < 0$). Тогда нужно перераспределить $H = c - d$ от богатых к бедным и средним.
Второй случай: средние зарабатывают больше среднего дохода ($(c - a) - (d - b) > 0$). Тогда нужно перераспределить $H = a - b$ от богатых и средних к бедным.
Сравнение в первом случае:
\[
\begin{aligned}
&G \quad \text{vs.} \quad H \\
&c - d + ad - bc \quad \text{vs.} \quad c - d \\
&ad - bc \quad \text{vs.} \quad 0 \\
&\frac{d}{c} \quad \text{vs.} \quad \frac{b}{a}
\end{aligned}
\]
 Так как кривая Лоренца выпукла, то $\frac{b}{a} = \tan\angle AOD < \frac{d}{c} = \tan\angle BOC$, откуда:
\[
\frac{d}{c} > \frac{b}{a} \quad \Rightarrow \quad G > H
\]
Сравнение во втором случае:
\[
\begin{aligned}
&G \quad \text{vs.} \quad H \\
&c - d + ad - bc \quad \text{vs.} \quad a - b \\
&(c - d + ad - bc) - (a - b) = [(c - a) - (d - b)](1 - b) + (a - b)(d - b)
\end{aligned}
\]
По условию второго случая:
$(c - a) - (d - b) > 0$ (средние имеют избыток дохода)
$1 - b > 0$,
$a - b > 0$,
$d - b > 0$
Все слагаемые положительны, следовательно:
\[
G - H > 0 \quad \Rightarrow \quad G > H
\]
Вывод: для трёх групп индекс Джини всегда больше индекса Робин Гуда.
а-3) Общий случай $n \geq 2$
Рассмотрим $n$-звенную кривую Лоренца и отметим граничную точку $(a,b)$, слева от которой располагаются жители, которым нужно добавить доход, а справа — те, у кого доход нужно уменьшить. Суммарно необходимо перераспределить долю $a - b$ совокупного дохода.
Теперь рассмотрим двузвенную кривую Лоренца с изломом в точке $(a,b)$ (зелёная ломаная). Для такой кривой индекс Джини равен индексу Робин Гуда и составляет $a - b$. Однако в силу выпуклости исходной кривой коэффициент Джини для вспомогательной кривой будет ниже, чем для исходной, при этом индексы Робин Гуда для обеих кривых совпадают.
Следовательно, коэффициент Джини для исходной кривой больше индекса Робин Гуда.
Так как кривая Лоренца выпукла, то $\frac{b}{a} = \tan\angle AOD < \frac{d}{c} = \tan\angle BOC$, откуда:
\[
\frac{d}{c} > \frac{b}{a} \quad \Rightarrow \quad G > H
\]
Сравнение во втором случае:
\[
\begin{aligned}
&G \quad \text{vs.} \quad H \\
&c - d + ad - bc \quad \text{vs.} \quad a - b \\
&(c - d + ad - bc) - (a - b) = [(c - a) - (d - b)](1 - b) + (a - b)(d - b)
\end{aligned}
\]
По условию второго случая:
$(c - a) - (d - b) > 0$ (средние имеют избыток дохода)
$1 - b > 0$,
$a - b > 0$,
$d - b > 0$
Все слагаемые положительны, следовательно:
\[
G - H > 0 \quad \Rightarrow \quad G > H
\]
Вывод: для трёх групп индекс Джини всегда больше индекса Робин Гуда.
а-3) Общий случай $n \geq 2$
Рассмотрим $n$-звенную кривую Лоренца и отметим граничную точку $(a,b)$, слева от которой располагаются жители, которым нужно добавить доход, а справа — те, у кого доход нужно уменьшить. Суммарно необходимо перераспределить долю $a - b$ совокупного дохода.
Теперь рассмотрим двузвенную кривую Лоренца с изломом в точке $(a,b)$ (зелёная ломаная). Для такой кривой индекс Джини равен индексу Робин Гуда и составляет $a - b$. Однако в силу выпуклости исходной кривой коэффициент Джини для вспомогательной кривой будет ниже, чем для исходной, при этом индексы Робин Гуда для обеих кривых совпадают.
Следовательно, коэффициент Джини для исходной кривой больше индекса Робин Гуда.
 б) Гладкая кривая Лоренца
б) Гладкая кривая Лоренца
 Аналогично рассмотрим новую кривую Лоренца, состоящую из двух отрезков, соединяющих точки $(0,0)$, $(a,b)$ и $(1,1)$, где $(a,b)$ — граничная точка (переход от нуждающихся в субсидии к тем, у кого доход нужно уменьшить). Для такой кусочно-линейной кривой индекс Робин Гуда равен индексу Джини и составляет $H = G = a - b$.
Поскольку построенная ломаная всюду лежит не ниже исходной кривой Лоренца (т.е. ближе к линии равенства), площадь между ней и диагональю превышает соответствующей площади для исходной кривой. Следовательно:
\[
G_{\text{исх}} > G_{\text{лом}} = H_{\text{лом}}
\]
В то же время, по построению, максимальное вертикальное отклонение у обеих кривых достигается в точке $(a,b)$ и равно $a - b$, поэтому:
\[
H_{\text{исх}} = H_{\text{лом}}
\]
Таким образом:
\[
G_{\text{исх}} > H_{\text{исх}}
\]
что доказывает неравенство между индексом Джини и индексом Робин Гуда для гладкой кривой Лоренца.
Аналогично рассмотрим новую кривую Лоренца, состоящую из двух отрезков, соединяющих точки $(0,0)$, $(a,b)$ и $(1,1)$, где $(a,b)$ — граничная точка (переход от нуждающихся в субсидии к тем, у кого доход нужно уменьшить). Для такой кусочно-линейной кривой индекс Робин Гуда равен индексу Джини и составляет $H = G = a - b$.
Поскольку построенная ломаная всюду лежит не ниже исходной кривой Лоренца (т.е. ближе к линии равенства), площадь между ней и диагональю превышает соответствующей площади для исходной кривой. Следовательно:
\[
G_{\text{исх}} > G_{\text{лом}} = H_{\text{лом}}
\]
В то же время, по построению, максимальное вертикальное отклонение у обеих кривых достигается в точке $(a,b)$ и равно $a - b$, поэтому:
\[
H_{\text{исх}} = H_{\text{лом}}
\]
Таким образом:
\[
G_{\text{исх}} > H_{\text{исх}}
\]
что доказывает неравенство между индексом Джини и индексом Робин Гуда для гладкой кривой Лоренца.
