- Определить $K$ можно одним из двух способов.
Способ 1. При эффективном распределении производства товар производят те страны, в которых альтернативные издержки его производства минимальны.
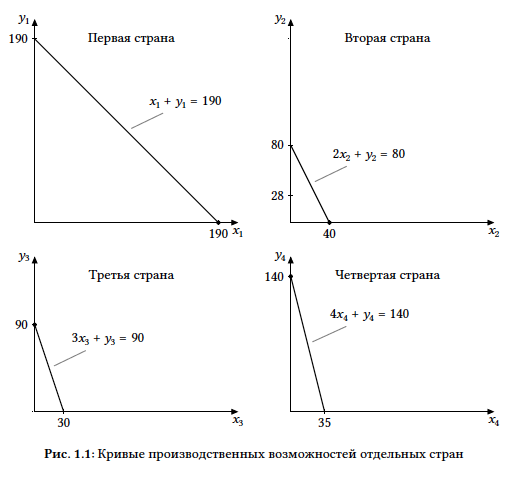
В данном случае альтернативные издержки производства Икса равны 1, 2, 3 и 4 единицы Игрека в странах соответственно. Значит, товар Икс производят страны 1 и 2, а товар Игрек –– страны 3 и 4. Таким образом, общее производство Икса равно $190 + 80/2 = 230$, общее производства Игрека
равно $90 + 140 = 230$. Следовательно, товары потребляются
в пропорции $1 ∶ 1$, то есть $K = 1$.
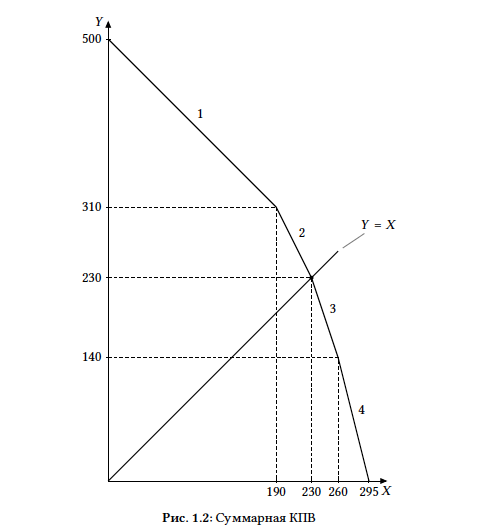
Способ 2. Тот же результат можно было получить, построив суммарную КПВ (Рис. 1.2). Точка на КПВ, в которой две страны производят только Икс –– это вторая точка излома КПВ (если считать слева направо), ее координаты –– $(230; 230)$. Через нее и начало координат проходит прямая с наклоном $1$ (отсюда получается $K = 1$).
В странах 1 и 2 производится Икс, и поэтому они не экспортируют Игрек. Страна 3 производит $90$ единиц Игрека, и поэтому она не может экспортировать $100$ единиц. Значит, «страна $N$» –– это страна 4.
- Поскольку страна 4 экспортирует $100$ единиц Игрека и производит $140$, для домашнего потребления остается $40$ единиц Игрека, а $40$ единиц Икса импортируется.
В отсутствие торговли (в условиях автаркии) страна 4 будет производить равное количество единиц Икса и Игрека (и потреблять столько же). Значит, $4x_4 + x_4 = 140$, откуда $x_4 =
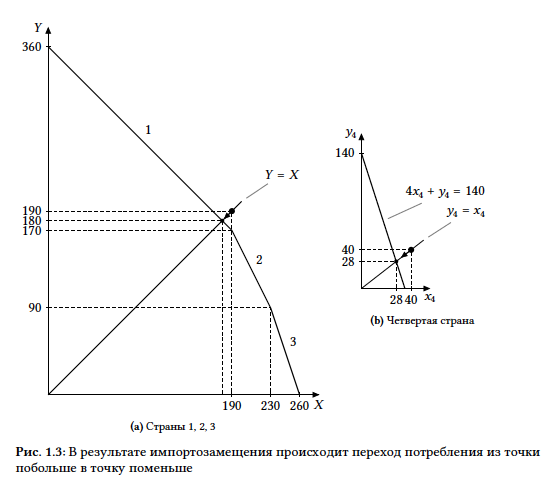
= y_4 = 28$. В условиях торговли страна потребляла по $40$ единиц Икса и Игрека. Значит, потребление комплектов из Икса и Игрека сократилось на $12$ единиц (Рис. 1.3b).
Этот результат не должен вызвать удивления: отказываясь от участия в торговле, страна лишает себя возможности покупать товар дешевле, чем ей обходится его производство.
- В условиях торговли со страной 4 страны 1, 2 и 3 в сумме потребляли $230 − 40 = 190$ единиц Икса и Игрека. После исключения страны 4 из торговли объемы потребления будут определяться пересечением суммарной КПВ стран 1, 2 и 3 и прямой $Y = X$.
Суммарная КПВ стран 1, 2 и 3 является ломаной, соединяющей точки $(0; 360)$, $(190; 170)$, $(230; 90)$, $(260; 0)$, она представлена на Рис. 1.3a. Поскольку точка излома $(190; 170)$ лежит ниже прямой $Y = X$, пересечение будет достигаться на первом участке КПВ. Первый участок описывается уравнением $Y = 360 − X$, значит, точка пересечения удовлетворяет уравнению $360 − X = X$, откуда $X = 180$. Значит, суммарное потребление комплектов из Икса и Игрека в трех странах уменьшилось на $190 − 180 = 10$ единиц.
Этот результат не должен вызвать удивления: когда одна из стран отказалась от участия в торговле, остальные страны потеряли возможность покупать товар, в котором она имеет сравнительное преимущество.
Альтернативное решение
а) Поскольку страны свободно торгуют товарами, решить задачу можно, сделав предположения о возможных мировых о ценах этих товаров.
Если бы $p_Y>p_X$, то все страны, максимизируя свой доход, производили бы только товар Игрек (при этом каждая из стран), что не обеспечит требуемый баланс между объемами потребления товаров и не удовлетворит условию задачи о том, что только две страны производят этот товар.
Если бы $p_X>4p_Y$, то все страны, максимизируя свой доход, производили бы только товар Икс, что также не обеспечит требуемый баланс между объемами потребления и не удовлетворит условию задачи о том, что только две страны производят этот товар.
Если бы $p_Y\le p_X<2p_Y$, то вторая, третья и четвертая страны, максимизируя свой доход, производили бы только товар Игрек, что также не удовлетворяет условию задачи.
Если бы $3p_Y< p_X\le 4p_Y$, то первая, вторая и третья страны, , максимизируя свой доход, производили бы только товар Икс, что также не удовлетворяет условию задачи.
Единственной возможностью, при которой две страны будут производить товар Икс и две страны - товар Игрек, является ситуация, когда мировые цены соотносятся следующим образом: $2p_Y\le p_X\le 3p_Y$. Тогда товар Икс будут производить первая и вторая страны, а товар Игрек – третья и четвертая. Следовательно, будет произведено $190+40=230$ единиц товара Икс и $90+140=230$ единиц товара Игрек. Откуда сразу следует пропорция, в которой эти товары потребляются странами: на каждую единицу товара Икс должна приходиться одна единица товара Игрек.
Заметим, что соотношение между мировыми ценами в этом случае можно было бы найти, например, из торгового баланса 4-ой страны, которая продаст 100 единиц товара Игрек ради приобретения 40 единиц товара Икс (в этом случае 4-ая страна потребит 40 единиц каждого товара). Следовательно, $100p_Y=40p_X$, или $p_X-2.5p_Y$
в) Подход к решению аналогичен решению пункта а).
Если бы $p_Y>p_X$, то все страны, максимизируя свой доход, производили бы только товар Игрек, что не обеспечит требуемый баланс между объемами потребления товаров.
Если бы $p_X>3p_Y$, то все страны, максимизируя свой доход, производили бы только товар Икс, что также не обеспечит требуемый баланс между объемами потребления товаров.
Если бы $p_Y\le p_X\le 3p_Y$, то 1-ая страна производила бы только товар Икс в объеме 190 единиц и для удовлетворения требуемого соотношения потребовалось бы произвести 190 единиц товара Игрек, однако, даже если бы при сложившихся рыночных ценах обе страны производили бы только Игрек, то смогли бы произвести не более $90+80=170$ единиц. Что также не обеспечит требуемый баланс между объемами потребления.
Единственной возможностью, когда можно будет удовлетворить этот баланс, если 1-ая страна будет производить оба товара. Это возможно только при $p_Y= p_X$. Тогда 2-ая и 3-я страны произведут только товар Игрек в объеме 170 единиц. Учитывая соотношение в объемах потребления товаров, найдем, сколько Иксов и Игреков должна произвести 1-ая страна: $y=170+y_1=190-y_1$, откуда $y_1=10, x_1=180$. То есть, всего 180 комплектов, состоящих Икса и Игрека, произведет мировой рынок, состоящий из 1-ой, 2-ой и 3-ей стран.
