Находим цены одних активов через цены других

Создано: 23.12.2025

Последнее изменение 05.02.2026

2

0

На фондовом рынке торгуется акция компании X, которая в ближайшие несколько лет не будет платить дивиденды. Цена акции в текущий момент равна \(X_0 = 220\). Кроме того, торгуются безрисковые, бескупонные облигации со сроком погашения через год и номиналом \(22\). Доходность по ним равна \(10\%\) годовых. Цену акции через 1 год обозначим за \(X_1\) (в текущий момент она неизвестна, и ваши ответы не могут от нее зависеть). Известно, что на рынке отсутствуют возможности для арбитража, откуда следует, что портфели активов, приносящие одинаковый поток доходов через год при каждом \(X_1\), сегодня должны стоить одинаково. Для решения задачи записывайте, как будущий доход от того или иного контракта (возможно, отрицательный) зависит от \(X_1\). Все цены контрактов, которые нужно найти в задаче, — это цены в текущий момент. а) (4 балла) Если инвестор A купит у инвестора B финансовый контракт 1, то он будет обязан купить у инвестора B одну акцию компании X через 1 год по цене 220. Найдите цену контракта 1. б) (4 балла) Контракт 2 дает своему владельцу право купить одну акцию компании X через 1 период по цене 220. Контракт 3 дает своему владельцу право продать одну акцию компании X через 1 год по цене 220. Найдите цену контракта 3, если цена контракта 2 в текущий момент равна 30. Подсказка: вам может помочь результат п. а). в) (4 балла) Теперь рассмотрим экзотический контракт 4, доход от которого зависит от будущей цены акции \(X_1\) так, как показано на графике ниже.

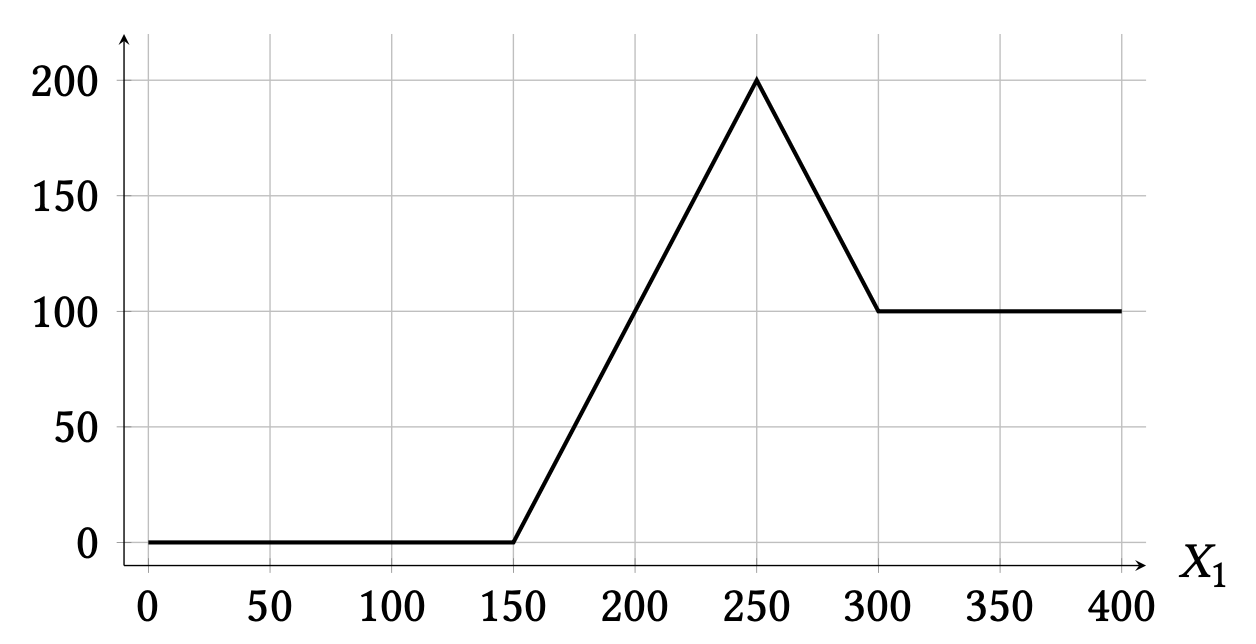
Схематичный график зависимости дохода контракта 4 от \(X_1\). Кроме того, известны цены других контрактов, которые дают право на покупку или продажу 1 акции компании X через год по определенным ценам:

Контракт	Дает право на	По цене	Цена контракта
5	покупку	150	80
6	покупку	250	10
7	продажу	250	190/11
8	покупку	300	1

Найдите цену контракта 4.

Решение и ответ

Обозначим цену контракта \(i\) сегодня как \(p_i\). Цена бескупонной облигации с номиналом 22 через год при доходности \(r=10\%\): \(\frac{22}{1+r}=\frac{22}{1.1}=20\).

а) Цена контракта 1

Контракт 1 обязывает через год купить акцию по 220, значит его будущий доход (payoff) равен \[ X_1 - 220. \] Рассмотрим два портфеля с одинаковым будущим доходом при любом \(X_1\):

Портфель A: 1 акция. Будущий доход: \(X_1\).
Портфель B: контракт 1 + 10 облигаций. Будущий доход: \((X_1-220)+10\cdot 22 = X_1\).

Доходы совпадают при каждом \(X_1\), значит при отсутствии арбитража цены сегодня равны: \[ 220 = p_1 + 10\cdot \frac{22}{1.1} = p_1 + 10\cdot 20 = p_1 + 200. \] Отсюда \(p_1 = 20\).

б) Цена контракта 3 при \(p_2=30\)

Контракт 2 — это опцион колл со страйком 220: payoff \(\max(X_1-220,0)\).
Контракт 3 — это опцион пут со страйком 220: payoff \(\max(220-X_1,0)\).

Заметим тождество для любого \(X_1\): \[ (X_1-220) + \max(220-X_1,0) = \max(X_1-220,0). \] То есть: колл = форвард (контракт 1) + пут (контракт 3).

По отсутствию арбитража цены сегодня удовлетворяют: \[ p_2 = p_1 + p_3. \] Подставляем \(p_2=30\) и найденное \(p_1=20\): \[ 30 = 20 + p_3 \;\Rightarrow\; p_3 = 10. \]

в) Цена контракта 4

По графику доход контракта 4 как функция \(X_1\) можно записать так: \[ f_4(X_1)= \begin{cases} 0, & X_1 \le 150,\\ 2(X_1-150), & 150 < X_1 \le 250,\\ 2(350-X_1), & 250 < X_1 \le 300,\\ 100, & X_1 \ge 300. \end{cases} \]

Контракты 5,6,8 — коллы (право купить), контракт 7 — пут (право продать). Их payoff:

5: \(\max(X_1-150,0)\)
6: \(\max(X_1-250,0)\)
7: \(\max(250-X_1,0)\)
8: \(\max(X_1-300,0)\)

Подберем коэффициенты \(a,b,c,d\), чтобы портфель \[ a\cdot (5) + b\cdot (6) + c\cdot (7) + d\cdot (8) \] давал тот же payoff, что и контракт 4, при любом \(X_1\). Подходящий набор (возможны короткие продажи) такой: \[ a=2,\quad b=-4,\quad c=0,\quad d=2. \] Тогда по отсутствию арбитража цена контракта 4 равна цене этого портфеля: \[ p_4 = 2\cdot 80 + (-4)\cdot 10 + 0\cdot \frac{190}{11} + 2\cdot 1 = 160 - 40 + 2 = 122. \]

Если хочется обойтись без отрицательных количеств, можно переписать равенство payoff так: \[ (4) + 4\cdot (6) = 2\cdot (5) + 2\cdot (8), \] откуда сразу: \[ p_4 + 4\cdot 10 = 2\cdot 80 + 2\cdot 1 \Rightarrow p_4 = 162 - 40 = 122. \]

Ответ: \(p_1=20\), \(p_3=10\), \(p_4=122\).