Администратору спортивного лагеря нужно расселить чётное количество детей из первого отряда по комнатам. В каждой комнате могут жить ровно 2 человека. Все дети — девочки, поэтому изначально возможна любая пара потенциальных соседей. У каждого из детей есть предпочтения на множестве потенциальных соседей, то есть каждый из ребят может упорядочить всех потенциальных соседей от наилучшего для себя до наихудшего. При этом, для каждого из ребят эти предпочтения строгие — не существует двух соседей, которые были бы одинаково хороши с точки зрения кого-либо из ребят. Предпочтения также являются транзитивными, то есть если для девочки верно, что $i$ лучше $j$ (обозначим это утверждение как $i \succ j$) и $j \succ k$, то для неё верно $i \succ k$.
После того, как администратор расселил ребят по комнатам, ребятам можно меняться соседями. Для этого двое детей должны подойти к администратору и сказать, что они хотят жить друг с другом больше, чем со своими текущими соседями. Назовём стабильным такое расселение ребят, при котором никакая пара ребят не хочет подойти к администратору для совершения обмена.
Примечание. Задача является примером применения дизайна механизмов, о котором можно узнать больше из материалов просветительского проекта РЭШ GURU.
а) Пусть администратору надо расселить ровно 4 ребёнка. Сколько всего расселений возможны?
б) Может ли в этом случае быть ровно одно стабильное расселение? А два? А три? Если вы считаете, что может, приведите пример. Если нет, докажите невозможность.
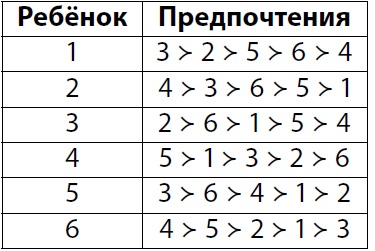
в) Предположим, что администратору нужно расселить 6 детей. Для удобства занумеруем их от 1 до 6. Их предпочтения представлены в таблице ниже. Выражение $i \succ j$ означает, что, по мнению ребёнка, сосед $i$ лучше соседа $j$. Найдите все стабильные расселения и докажите, что других не существует.
Автор
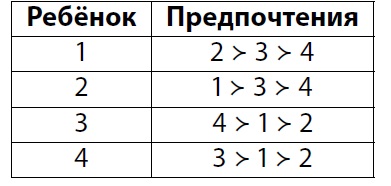Приведём пример с двумя стабильными расселениями. В этом случае стабильные распределения — это 12 и 14. Заметим, что в расселении 12 есть два ребёнка (1 и 3), которые живут с лучшим для себя соседом, поэтому не будут меняться. Тогда поменяться могут только 2 и 4, но они худшие варианты друг для друга, поэтому меняться не будут. Аналогично, в расселении 14 есть два ребёнка (2 и 4), которые живут с лучшим для себя соседом, поэтому не будут меняться. Тогда поменяться могут 1 и 3, но они худшие варианты друг для друга, поэтому меняться не будут. Расселение 13 не будет стабильным, поскольку захотят поменяться, например, 1 и 2.
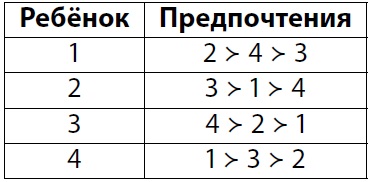Теперь докажем, что не может быть трёх стабильных распределений. Заметим, что если два человека живут с худшими для себя соседями, то они хотели бы поменяться с кем угодно. Также заметим, что если два человека — лучшие соседи друг для друга, то любое распределение, где они не живут вместе, не может быть стабильным.
Всего есть 3 расселения и 4 человека. Значит, есть хотя бы одно расселение, где сразу 2 человека живут с худшим для себя соседом. Любители комбинаторики могут вспомнить принцип Дирихле.
Если они живут не друг с другом, то они могут поменяться, значит, расселение не стабильно. Если же они живут друг с другом, то один из них может поменяться с кем-то в другой паре, если эта пара не является лучшими соседями друг для друга. Если хотя бы для одного из оставшейся пары сосед не лучший, то он согласится поменяться с кем-то из худших друг для друга соседей, поэтому такое расселение не будет стабильным.
Остался последний случай, при котором эта пара — лучшие друг для друга соседи. Тогда они всегда живут друг с другом в стабильном расселении, значит, остальные расселения не стабильны. Таким образом, 3 стабильных расселения невозможны
в) Рассмотрим предпочтения, описанные в условии.
Шаг 1. Рассмотрим решение индивида i. Если для индивида j он является лучшим соседом, то индивид i не выберет в стабильном расселении никого хуже с его точки зрения, чем j, потому что всегда можно решить жить с j. Учитывая это, вычеркнем невозможные пары. На картинке ниже красным зачёркнуты невозможные пары. Затем те же пары зачёркнуты оранжевым (каждая пара встречается дважды).
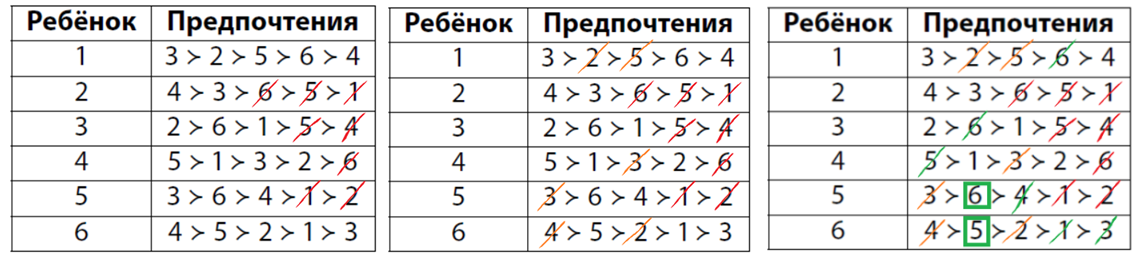Шаг 2. Заметим, что из оставшихся возможных опций 5 и 6 — лучшие друг для друга (обведено зелёным на картинке). Значит, они будут жить вместе. Тогда зачеркнём зелёным невозможные пары из числа оставшихся.
Шаг 3. Остаётся заметить, что возможны два стабильных расселения оставшихся —13 24 и 14 23. В первом случае 1 и 2 живут с лучшими для себя соседями, а 3 и 4 не готовы меняться. Во втором случае 3 и 4 живут с лучшими для себя соседями, а 1 и 2 не готовы меняться.
Ответ. Всего 2 стабильных расселения —13 24 56 и 14 23 56.
