Total Costs

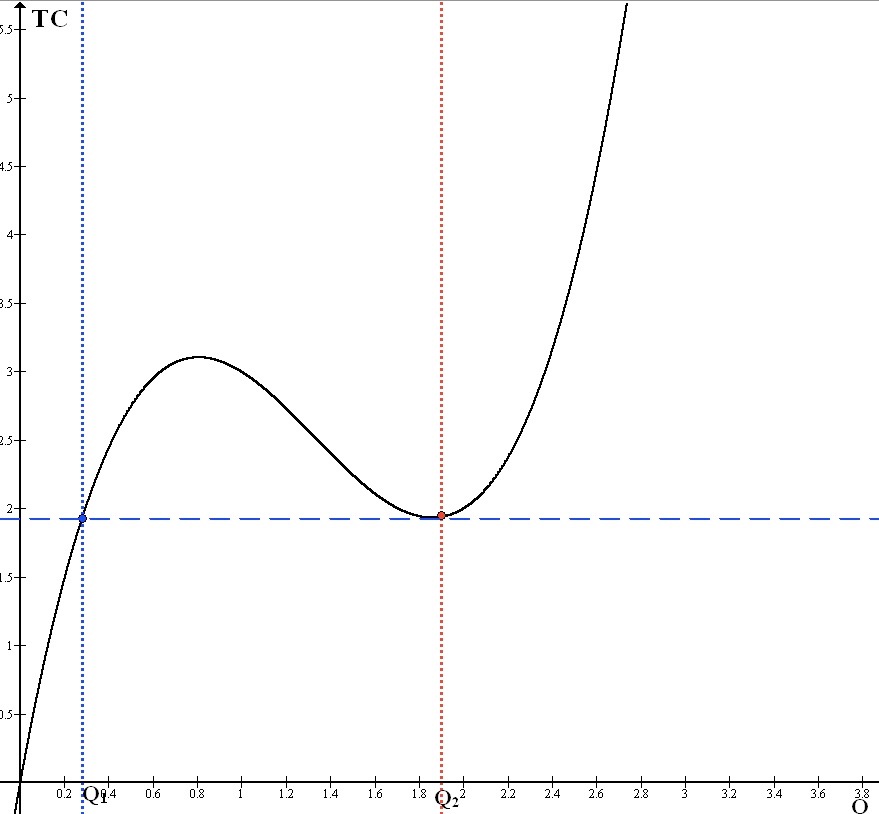Рассмотрим промежуток убывания произвольной функции. На этом промежутке найдём точку локального минимума- $Q_2$. Тогда для любого $Q$ из промежутка $[Q_1;Q_2]$ можно произвести $Q_2$ и понести издержки $TC(Q_2)$, при этом $TC(Q_2)\le TC(Q)$. Следовательно, если рациональный производитель желает продать $Q$ ,то он будет производить $Q_2$, но продавать $Q$. Таким образом до $Q_1$ $TC$ не убывает, на промежутке $[Q_1;Q_2]$ $TC=const$ , после $Q_2$ - не убывает, ч.т.д.