Город Капучиновск представляет собой квадрат, разбитый на 16 одинаковых по площади квадратных районов $(A1, \ldots , D4)$. Кофейня «Шоко-хауз» (ШХ) расположена в районе $B2$, а кофейня «Кофебакс» (КБ) - в квартале $D4$. В каждом районе живут ровно 120 человек, каждый из которых ежедневно пьет одну чашку кофе. Если в районе, где человек живет, есть кофейня, то он ходит в неё, а иначе выбирает ближайшую кофейню к дому. Если на одинаковом расстоянии от какого-то района расположено несколько кофеен, то жители этого района распределяются между ближайшими кофейнями поровну.
Из-за специфики системы улиц и заграждений в Капучиновске переход между соседними районами возможен только через середину границы между ними, то есть каждый житель города перемещается по нему как ладья по шахматной доске, измеряя при этом расстояния количеством переходов через границу района. Например, жителям района $A4$ нет разницы, в какую кофейню ходить - кратчайший путь до каждой занимает три перехода (пути показаны на рисунке).
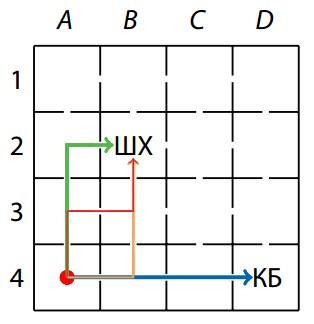Каждая кофейня получает прибыль в размере 1 доллар с каждой проданной чашки кофе.
а) [3 балла] Найдите значения прибыли, которую получают кофейни «Шоко-хауз» и «Кофебакс».
б) [5 баллов] Город Дабл-Капучиновск отличается от Капучиновска только тем, что он имеет форму квадрата $6\times 6$ (в нём 36 районов: $A1, ..., F6$). Кофейня «Шоко-хауз» расположена в квартале $C2$, «Кофебакс» в квартале $E5$. Фирма «Старладница» собирается построить кофейню в этом городе, при том что законодательство запрещает располагать кофейню в соседнем (по вертикали или горизонтали) районе с уже существующей. Где «Старладница» должна построить кофейню для получения максимальной прибыли, если она ожидает, что после этого будет конкурировать только с «Шоко-хаузом» и «Кофебаксом»?
в) [5 баллов] После того как «Старладница» построила свою кофейню в районе, определенном в пункте $\textbf{б)}$, на рынок решила зайти фирма «Суперчашка», которая также намерена построить кофейню в одном из районов города. Где ей следует это сделать, чтобы получить максимальную прибыль?
г) [7 баллов] Предположим, владелец «Старладницы» предвидел появление на рынке «Суперчашки» и выбирал место для своей кофейни с учетом наличия трёх конкурентов: «Шоко-хауза», «Кофебакса» и «Суперчашки». Как это повлияет на ответы пунктов $\textbf{б)}$ и $\textbf{в)}$?
Каждая кофейня получает прибыль в размере 1 доллар с каждой проданной чашки кофе.
а) [3 балла] Найдите значения прибыли, которую получают кофейни «Шоко-хауз» и «Кофебакс».
б) [5 баллов] Город Дабл-Капучиновск отличается от Капучиновска только тем, что он имеет форму квадрата $6\times 6$ (в нём 36 районов: $A1, ..., F6$). Кофейня «Шоко-хауз» расположена в квартале $C2$, «Кофебакс» в квартале $E5$. Фирма «Старладница» собирается построить кофейню в этом городе, при том что законодательство запрещает располагать кофейню в соседнем (по вертикали или горизонтали) районе с уже существующей. Где «Старладница» должна построить кофейню для получения максимальной прибыли, если она ожидает, что после этого будет конкурировать только с «Шоко-хаузом» и «Кофебаксом»?
в) [5 баллов] После того как «Старладница» построила свою кофейню в районе, определенном в пункте $\textbf{б)}$, на рынок решила зайти фирма «Суперчашка», которая также намерена построить кофейню в одном из районов города. Где ей следует это сделать, чтобы получить максимальную прибыль?
г) [7 баллов] Предположим, владелец «Старладницы» предвидел появление на рынке «Суперчашки» и выбирал место для своей кофейни с учетом наличия трёх конкурентов: «Шоко-хауза», «Кофебакса» и «Суперчашки». Как это повлияет на ответы пунктов $\textbf{б)}$ и $\textbf{в)}$?Сложность
Автор
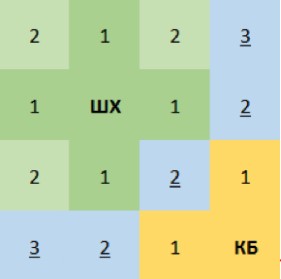Чтобы найти прибыль каждой кофейни, достаточно для каждого квартала города определить, где будут пить кофе его жители. Это можно сделать разными способами. Например, можно отметить на рисунке одним цветом все кварталы, жители которых ходят в одну кофейню. Делать это можно в следующей последовательности: сначала для каждой кофейни отметить её цветом все кварталы на расстоянии 1 от неё, затем на расстоянии 2 и т.д. Если в процессе такой разметки окажется, что какой-либо квартал находится на одинаковом расстоянии от обеих кофеен, следует отметить его третьим цветом. После того, как каждый квартал будет окрашен, останется только посчитать прибыли кофеен: 120 за каждый квартал, окрашенный в цвет этой кофейни, плюс $120/2=60$ за каждый квартал третьего цвета. В качестве проверки правильности ответа можно сложить прибыли обеих кофеен и проверить, равняется ли сумма $4\cdot 4\cdot 120=1920$ - общему числу жителей в городе.
Ответ: прибыль «Шоко-хауза» равна 1260, «Кофе-бакса» – 660.
Пункт б
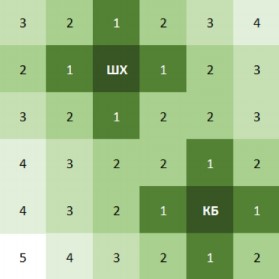Как и в предыдущем пункте, ответ можно получить разными способами. К примеру, можно снова отметить на схеме города расстояние от каждого квартала до ближайшей уже построенной кофейни, отдельно отметив кварталы, где строительство невозможно. Глядя на такую карту, можно попытаться угадать, где следует построить новую кофейню: логично предположить, что ее выгоднее строить в той части города, жителям которой приходится дальше всех ходить за кофе. Строить кофейню следует так, чтобы в нее ходило как можно больше людей: не только из тех кварталов, до которых в «Старладницу» ходить ближе всего, но и из тех, откуда после ее открытия будет одинаково близко ходить в несколько кофеен. В данном случае наиболее оптимальным кварталом для открытия кофейни является C4 – это можно проверить, сравнив прибыли «Старладницы» в случае открытия в C4 и в любом близлежащем квартале. Расчёты приведены в таблице:
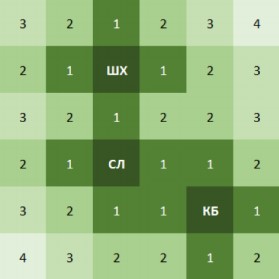Аналогично предыдущему пункту, можно нарисовать такую же карту с учетом трёх построенных кофеен, а затем таким же образом определить наиболее прибыльное местоположение. Расчёты также приведены в таблице:
